Sean and I have been discussing rolling methods for ability scores, particularly in the context of PCs vs. henchmen. Consider the two following methods for generating a set of abilities (sourced from the 2e PH, p. 13):
For most NPCs and hirelings, I employ Method II, which tends to generate more averages sets. I don't use any re-roll caveat for NPCs. They get what they get.
Because, in our campaign, henchmen have the ability to replace fallen PCs over the long-term, we want to make sure we're in agreement on the rolling method to use. Most AD&D players intuitively know that Method V is more likely to generate high scores (15+) than Method II, but what if we evaluate the methods more deeply? Let's say, for example, that we're looking to create a ranger, which requires two scores of 14 or higher and two additional scores of 13 or higher.
I wrote a quick app to generate random sets of ability scores using both methods. Scores within each set are arranged from highest to lowest, with sets that qualify for the ranger class marked with a letter r. Here are results for ten sets of scores for each method:
This time, one ranger for Method II, four rangers for Method V (an opposite result). Obviously, we need more data. I'll have the application roll 100 sets for each method and take the averages (rounded down to whole numbers):
These are actually really close; in fact, the total number of ability points is the same with both methods. Through another few runs, I was able to verify that these exact averages still hold even with a very high (10,000) number of sets.
But the averages don't tell the full story. Again, we know from intuition that there's going to be tangible variance between the methods. If it's not in the total number of points, then where?
For starters, we know that, in order to get stuck with a score of 3 using Method II, we need to roll six 1s in a row. That means 6^6, or one in 46,656 scores. To get equally unlucky with Method V, you only need to roll four straight 1s, or 6^4, which is one in 1,296 scores.
That's a major difference: you're almost 40 times more likely to end up with a score of 3 using Method V (the 4d6 method) compared with Method II (the 3d6-twice method).
Let's see what the distribution of scores is over ten sets of scores using each rolling method:
That looks reasonable: fewer high but also fewer low scores when using Method II. How about for 1,000 sets?
Now we're starting to see the numbers at work. A thousand sets contain 6,000 individual scores; we have three scores of 3 using Method V, and none using Method II. Given that we were expecting only one in 46,656 scores with Method II but about one in 1,296 scores with Method V to result in a lowly 3, these results look pretty solid, though our sample sizes are still small enough that we're hitting a fair degree of variance.
Here are the totals for 100,000 sets:
For Method II, fifteen out of 600,000 scores ended up as 3, or one in 40,000, which is very close to the one in 46,656 ratio that we expect to normalize to over the long term. For Method V, we had 473 scores of 3, which is about one in 1,268... extremely close to the normalized ratio of one in 1,296.
If we add up all the scores of 7 or lower, Method II only generated 15,716 while Method V produced a whopping 34,063. If we add up all the scores of 15 or higher, Method II gave us 106,252 while Method V resulted in 138,832.
The takeaways are that you're more than twice as likely to get bad scores (7 or lower) with the 4d6 method, but only about 30% more likely to get high scores (15 and above). Method V, however, is almost twice as likely to generate very high scores (17 or 18), while Method II is far more likely to hit in the average range of 10 through 14.
Finally, here's a plot graph of the 100,000 set results, which makes everything nice and clear:
Though Sean and I still haven't decided exactly how to handle scores for a new henchmen, the above data definitely provides the right ammunition to help us make the best decision for our campaign. As an extra bonus, here are score distributions for two additional rolling methods described in the PH, along with an additional graph that charts all four methods.
...along with the score distributions of the two new methods:
...and the final graph depicting all four methods:
(If you made it to the end of this post, congratulations!)
- Method II. Roll 3d6 twice and take the higher of the two values.
- Method V. Roll 4d6, discard the lowest roll, and add up the other three.
For most NPCs and hirelings, I employ Method II, which tends to generate more averages sets. I don't use any re-roll caveat for NPCs. They get what they get.
Because, in our campaign, henchmen have the ability to replace fallen PCs over the long-term, we want to make sure we're in agreement on the rolling method to use. Most AD&D players intuitively know that Method V is more likely to generate high scores (15+) than Method II, but what if we evaluate the methods more deeply? Let's say, for example, that we're looking to create a ranger, which requires two scores of 14 or higher and two additional scores of 13 or higher.
I wrote a quick app to generate random sets of ability scores using both methods. Scores within each set are arranged from highest to lowest, with sets that qualify for the ranger class marked with a letter r. Here are results for ten sets of scores for each method:
Method II results (3d6 twice, take higher):Four rangers for Method II, only two for Method V. This are very small samples sizes, so let's run them again to observe the variance:
16 14 13 13 11 11 (r)
16 13 12 12 10 8
15 14 13 11 9 8
16 15 14 12 11 11
14 14 13 13 12 11 (r)
13 11 11 11 9 5
15 15 15 13 12 8 (r)
15 14 14 12 12 8
13 12 12 11 10 8
16 14 14 13 12 11 (r)
Method V results (4d6 drop lowest):
15 13 13 12 12 12
14 14 12 10 10 8
16 13 12 12 9 4
17 15 13 11 11 7
14 14 12 9 9 8
14 14 12 11 8 7
17 14 13 12 11 7
15 12 11 10 9 8
16 14 13 13 10 10 (r)
15 15 14 13 10 8 (r)
Method II results (3d6 twice, take higher):
13 12 11 11 11 6
14 13 13 12 12 12
14 13 13 12 12 11
17 16 12 11 10 9
13 13 13 12 11 10
15 15 12 10 9 8
17 16 12 11 9 8
15 14 14 10 9 9
16 16 15 15 14 9 (r)
17 13 13 13 12 12
Method V results (4d6 drop lowest):
15 12 11 11 10 9
15 14 13 12 12 7
15 13 11 11 11 9
16 14 12 11 10 8
14 14 13 13 12 12 (r)
15 15 14 13 11 10 (r)
17 14 14 14 13 11 (r)
16 16 15 12 10 8
15 15 14 13 12 5 (r)
18 14 13 12 9 9
This time, one ranger for Method II, four rangers for Method V (an opposite result). Obviously, we need more data. I'll have the application roll 100 sets for each method and take the averages (rounded down to whole numbers):
Method II averages:
15 13 12 11 10 9
Method V averages:
15 14 12 11 10 8
These are actually really close; in fact, the total number of ability points is the same with both methods. Through another few runs, I was able to verify that these exact averages still hold even with a very high (10,000) number of sets.
But the averages don't tell the full story. Again, we know from intuition that there's going to be tangible variance between the methods. If it's not in the total number of points, then where?
For starters, we know that, in order to get stuck with a score of 3 using Method II, we need to roll six 1s in a row. That means 6^6, or one in 46,656 scores. To get equally unlucky with Method V, you only need to roll four straight 1s, or 6^4, which is one in 1,296 scores.
That's a major difference: you're almost 40 times more likely to end up with a score of 3 using Method V (the 4d6 method) compared with Method II (the 3d6-twice method).
Let's see what the distribution of scores is over ten sets of scores using each rolling method:
Method II totals:
3s: 0
4s: 0
5s: 0
6s: 0
7s: 0
8s: 2
9s: 6
10s: 4
11s: 5
12s: 12
13s: 7
14s: 12
15s: 6
16s: 6
17s: 0
18s: 0
Method V totals:
3s: 0
4s: 0
5s: 0
6s: 2
7s: 2
8s: 2
9s: 6
10s: 3
11s: 3
12s: 12
13s: 9
14s: 5
15s: 10
16s: 3
17s: 3
18s: 0
That looks reasonable: fewer high but also fewer low scores when using Method II. How about for 1,000 sets?
Method II totals:
3s: 0
4s: 2
5s: 11
6s: 36
7s: 101
8s: 257
9s: 424
10s: 629
11s: 839
12s: 979
13s: 926
14s: 727
15s: 513
16s: 313
17s: 184
18s: 59
Method V totals:
3s: 3
4s: 25
5s: 51
6s: 99
7s: 194
8s: 269
9s: 451
10s: 585
11s: 697
12s: 794
13s: 740
14s: 737
15s: 586
16s: 430
17s: 240
18s: 99
Now we're starting to see the numbers at work. A thousand sets contain 6,000 individual scores; we have three scores of 3 using Method V, and none using Method II. Given that we were expecting only one in 46,656 scores with Method II but about one in 1,296 scores with Method V to result in a lowly 3, these results look pretty solid, though our sample sizes are still small enough that we're hitting a fair degree of variance.
Here are the totals for 100,000 sets:
Method II totals:
3s: 15
4s: 184
5s: 1056
6s: 3819
7s: 10642
8s: 24747
9s: 43524
10s: 65439
11s: 84711
12s: 94523
13s: 92145
14s: 72943
15s: 51490
16s: 32525
17s: 16626
18s: 5611
Method V totals:
3s: 473
4s: 1917
5s: 4722
6s: 9581
7s: 17370
8s: 29011
9s: 41925
10s: 56347
11s: 68252
12s: 77520
13s: 79661
14s: 74389
15s: 60690
16s: 43464
17s: 25012
18s: 9666
For Method II, fifteen out of 600,000 scores ended up as 3, or one in 40,000, which is very close to the one in 46,656 ratio that we expect to normalize to over the long term. For Method V, we had 473 scores of 3, which is about one in 1,268... extremely close to the normalized ratio of one in 1,296.
If we add up all the scores of 7 or lower, Method II only generated 15,716 while Method V produced a whopping 34,063. If we add up all the scores of 15 or higher, Method II gave us 106,252 while Method V resulted in 138,832.
The takeaways are that you're more than twice as likely to get bad scores (7 or lower) with the 4d6 method, but only about 30% more likely to get high scores (15 and above). Method V, however, is almost twice as likely to generate very high scores (17 or 18), while Method II is far more likely to hit in the average range of 10 through 14.
Finally, here's a plot graph of the 100,000 set results, which makes everything nice and clear:
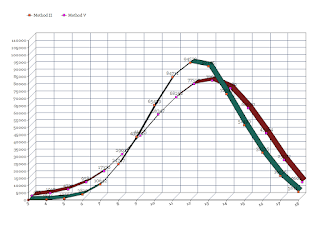 |
| Click to enlarge |
Though Sean and I still haven't decided exactly how to handle scores for a new henchmen, the above data definitely provides the right ammunition to help us make the best decision for our campaign. As an extra bonus, here are score distributions for two additional rolling methods described in the PH, along with an additional graph that charts all four methods.
- Method I. Roll 3d6 for each score.
- Method IV. Roll 3d6 twelve times, and take the six highest values.
Method II averages:
15 13 12 11 10 9
Method V averages:
15 14 12 11 10 8
Method I averages:
14 12 11 9 8 6
Method IV averages:
15 13 12 12 11 10
...along with the score distributions of the two new methods:
Method I totals:
3s: 2817
4s: 8353
5s: 16620
6s: 27915
7s: 41657
8s: 58653
9s: 68882
10s: 74966
11s: 74945
12s: 69277
13s: 58329
14s: 41804
15s: 27916
16s: 16701
17s: 8340
18s: 2825
Method IV totals:
3s: 0
4s: 0
5s: 0
6s: 1
7s: 129
8s: 2063
9s: 14860
10s: 50573
11s: 98940
12s: 123988
13s: 114935
14s: 83276
15s: 55540
16s: 33591
17s: 16596
18s: 5508
...and the final graph depicting all four methods:
 |
| Click to enlarge |
(If you made it to the end of this post, congratulations!)

No comments:
Post a Comment
Note: Only a member of this blog may post a comment.